先說說運算式有哪些表示法好了!
1. 前置(Prefix)運算式:
運算子放在兩個運算元前面,沒有括號,不易閱讀。
2. 中置(Infix)運算式:
運算子放在兩個運算元之間,可以有括號,最容易閱讀,例如a+b/d這樣的式子
3. 後置(Postfix)運算式:
運算子是放在兩個運算元之後,沒有括號,不易閱讀,後序表示式又稱之為逆向波蘭表示式(Reverse polish notation),它是由波蘭的數學家盧卡謝維奇提出,例如(a+b)*(c+d)這個式子,表示為後序表示式時是ab+cd+*。
運算式轉換分為中序轉前序和中序轉後序表示法,其轉換步驟十分相似,其差異只在運算子是位在運
算元前或後。例如:中序運算式,如下:
A*(B+C)
• 上述運算式轉換成前序和後序表示法的步驟,以運算子優先順序來進行處理,如下圖所示:
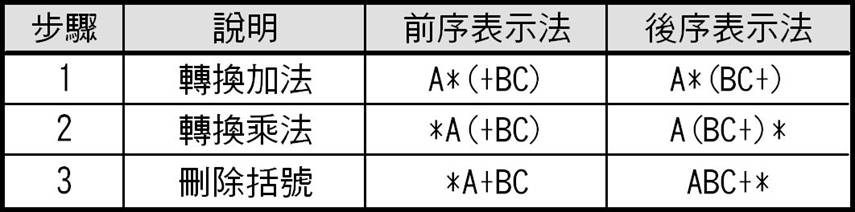
另一種方法是先替中序運算式加上完整括號來確認運算的優先順序,如下所示:
中序運算式: A+B*(C+D)-E
加上括號的中序運算式: ((A+(B*(C+D)))-E)
• 上述是加上括號的中序運算式,現在只需從最中間的括號開始,將運算子移到右括號的位置且刪除右號,直到刪除所有右括號為止,如下所示:
將運算子搬移到右括號: ((A(B(CD+*+E-
刪除所有的左括號: ABCD+*+E-
所以A-B/C*(D+E)先用括號化之後變為(A-((B/C)*(D+E)))
去括號後變為ABC/DE+*-
(a*(b+c) – d )中序表示法轉換成後序表示法的結果為何?
(a)abc*+-d (b)ab+c*d- (c)ab+c*-d (d)abc+*d-
九十四年公務人員初等考試試題資料處理大意
例子:a+b*d+c/d
解法
依演算法的輸出過程如下:
| OP | STACK | OUTPUT |
| ( | ( | – |
| a | ( | a |
| + | (+ | a |
| b | (+ | ab |
| ) | – | ab+ |
| * | * | ab+ |
| ( | *( | ab+ |
| c | *( | ab+c |
| + | *(+ | ab+c |
| d | *(+ | ab+cd |
| ) | * | ab+cd+ |
| – | – | ab+cd+* |
C的實作
#include <stdio.h>
#include <stdlib.h>
#define MAX 80
void inToPostfix(char*, char*); // 中序轉後序
int priority(char); // 運算子優先權
int main(void) {
char infix[MAX] = {'0'};
char postfix[MAX]= {'0'};
printf("中序運算式:");
scanf("%s", infix);
inToPostfix(infix, postfix);
int i;
for(i = 0; postfix[i] != '0'; i++) {
printf("%c", postfix[i]);
}
return 0;
}
void inToPostfix(char* infix, char* postfix) {
char stack[MAX] = {'0'};
int i, j, top;
for(i = 0, j = 0, top = 0; infix[i] != '0'; i++) switch(infix[i]) {
case '(': // 運算子堆疊
stack[++top] = infix[i];
break;
case '+': case '-': case '*': case '/':
while(priority(stack[top]) >= priority(infix[i])) {
postfix[j++] = stack[top--];
}
stack[++top] = infix[i]; // 存入堆疊
break;
case ')':
while(stack[top] != '(') { // 遇 ) 輸出至 (
postfix[j++] = stack[top--];
}
top--; // 不輸出 (
break;
default: // 運算元直接輸出
postfix[j++] = infix[i];
}
while(top > 0) {
postfix[j++] = stack[top--];
}
}
int priority(char op) {
switch(op) {
case '+': case '-': return 1;
case '*': case '/': return 2;
default: return 0;
}
}
上例取材自中序式轉後序式(前序式)
在106 年 – 特種考試地方政府公務人員考試/計算機概要也有中序轉後序的考古題,至於中序轉後序線上轉換的程式,後續再看能不能找到。
(a*(b+c)-d)中序表示法轉換成後序表示法的結果為何?
(A)abc+*d-
(B) bc*+-d
(C) ab+c*-d
(D) ab+c*d-
答案:A
相關程式設計文章:
※Python 圖形使用者介面程式設計
※50個 C# 工作面試常見問題

1 則留言