
二元搜尋樹是建立在樹節點鍵值的大小上。左子樹的所有鍵值均小於樹根的鍵值,右子樹所有鍵值均大於樹根的鍵值。而高度平衡二元搜尋樹則又定義某一個節點右子樹跟左子樹的高度,高度差的絕對值要小於等於 1,否則需要做調整,但調整的方法,最後必須維持二元搜尋樹的特質。在建立二元搜尋樹時,如果鍵值分別是 50、40、60、30、45。此時若再加入 20,此二元搜尋樹的高度平衡原則就會被破壞。請問根據高度平衡的原則去調整後,最後的二元搜尋樹的前序走訪的結果為何?
(A)203040504560 (B)403020455060 (C)504030602045 (D)403020504560
答案:(D)
最近看到考試院有新的公佈如下:
112年地方特考增列需用名額503人,加上原本公告的需用名額,總計需用名額為2438人。
考試院院會今(23)日通過,112年特種考試地方政府公務人員考試增列需用名額503人,總計需用名額為2,438人,其中三等考試1330人、四等考試931人、五等考試177人。各類科增列需用名額的具體情形,將於考選部全球資訊網另行公告。
考試院表示,112年地方特考原本公告需用名額為1935人,其中三等考試1068人、四等考試730人、五等考試137人。依據行政院人事行政總處再次提報缺額,增列需用名額503人(三等考試262人、四等考試201人、五等考試40人)。
雖說地方特考報名時間已過,也即將在12月到來的時候考試,但是有這個好消息也是不錯的,我們還是把焦點轉回到未來的113年初等考試吧!
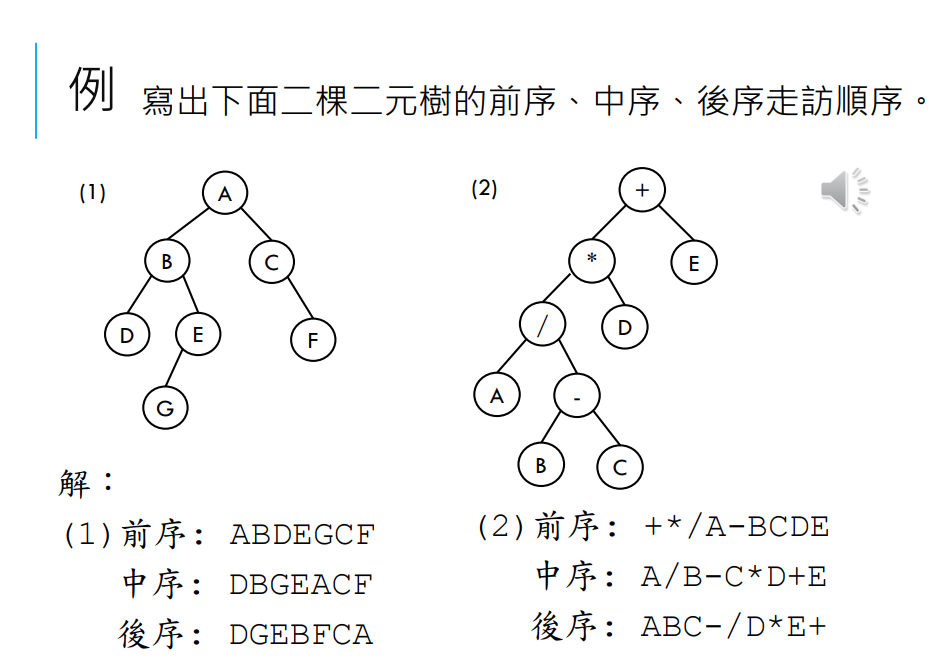
說到二元搜尋樹的概念,就請各位回頭看大叔的第18課:C 中的二元樹,如果要探訪二元樹的走訪可以看下面的說明:
資料讀取一遍的結果有DLR, DRL, LDR, LRD, RDL及RLD
若限制節點的左子樹比右子樹先走訪:
- DLR前序 (preorder)
- LDR中序 (inorder)
- LRD後序 (postorder)
上圖的說明應該可以知道二元搜尋樹的前序走訪是怎麼走法了,現在回到題目上如果鍵值分別是 50、40、60、30、45。此時若再加入 20,高度平衡二元搜尋樹會長怎樣?
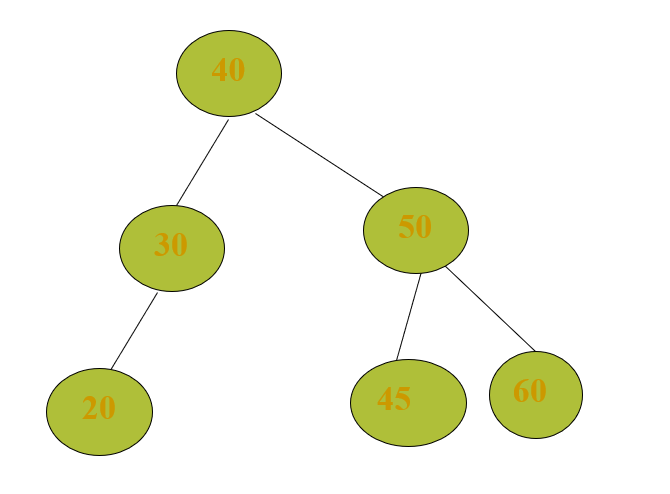
是的,變成這樣的二元樹,依照提議前序走訪的結果就是40->30->20->50->45->60
你會了嗎?不會可以再留言問我喔~