多年以前我一直想成為寫C語言教學的工作達人,記得那是13年前的事了,那時待在彩色濾光片廠擔任製造資訊工程師,有空的時候就寫一些部落格文章,但沒有專一性,什麼都寫,可能怕寫C語言教學沒有賺頭吧,後來我就擱置了,我的工作一直跟C語言沒關係,直到最近在思考幫助投考公職考試的朋友能夠更了解資訊類科的部份,所以我初測了一下112 年公務人員初等考考試試題統計類科的資料處理大意,我碰到了一個二元搜尋樹的高度平衡二元搜尋樹錯誤,現在回想起來感覺C語言還是有它存在的必要性,在程式語言排名TIOBE Index中排名第二,不容小覷,所以我今天要來繼續分享第18課:C 中的二元樹。
「二元樹」是計算機科學最重要的概念,甚至可以說:二元樹開創了計算機科學。像是排序資料結構 Binary Search Tree 、極值資料結構 Heap 、資料壓縮 Huffman Tree 、 3D 繪圖 BSP Tree ,這一大堆稀奇古怪的術語,通通都是二元樹。二元樹的應用相當廣泛,是資工系學生必學的基礎概念。也因為是基礎概念,所以幾乎是必考的題型。但說真的,我實作很少寫過這種程式,但或許在我的現實人生中或許已在使用這個概念也說不定。這篇文章除了翻譯www.cprogramming.com的資料外,我還會加上高度平衡二元搜尋樹的概念,我翻過很多書籍跟文件,發現Joseph’s blog寫的我看的最懂,錯誤應該也是最少的地方,也會轉載一部份內容分享在這裡讓你知道。
二元樹
在電腦科學中,二元樹(英語:Binary tree)是每個節點最多只有兩個分支(即不存在分支度大於2的節點)的樹結構。通常分支被稱作「左子樹」或「右子樹」。二元樹的分支具有左右次序,不能隨意顛倒。
二元樹的第層至多擁有2i-1個節點;深度為的二元樹至多總共有2k+1-1個節點(定義根節點所在深度k0=0),而總計擁有節點數符合的,稱為「滿二元樹」;深度為有個節點的二元樹,若且唯若其中的每一節點,都可以和深度的滿二元樹,序號1到的節點一對一對應時,稱為完全二元樹。對任何一棵非空的二元樹,如果其葉片(終端節點)數為n0,分支度為2的節點數為n2,則n0=n2+1。
與普通樹不同,普通樹的節點個數至少為1,而二元樹的節點個數可以為0;普通樹節點的最大分支度沒有限制,而二元樹節點的最大分支度為2;普通樹的節點無左、右次序之分,而二元樹的節點有左、右次序之分。
二元樹通常作為資料結構應用,典型用法是對節點定義一個標記函數,將一些值與每個節點相關聯。這樣標記的二元樹就可以實現二元搜尋樹和二元堆積,並應用於高效率的搜尋和排序。
二元搜尋樹
二元搜尋樹(英語:Binary Search Tree),也稱為有序二元樹(ordered binary tree)或排序二元樹(sorted binary tree),是指一棵空樹或者具有下列性質的二元樹:
- 若任意節點的左子樹不空,則左子樹上所有節點的值均小於它的根節點的值;
- 若任意節點的右子樹不空,則右子樹上所有節點的值均大於它的根節點的值;
- 任意節點的左、右子樹也分別為二元搜尋樹;
二元搜尋樹相比於其他資料結構的優勢在於尋找、插入的時間複雜度較低。為O(㏒ n)。二元搜尋樹是基礎性資料結構,用於構建更為抽象的資料結構,如集合、多重集、關聯陣列等。
二元搜尋樹的尋找過程和次優二元樹類似,通常採取二元鏈結串列作為二元搜尋樹的儲存結構。中序遍歷二元搜尋樹可得到一個關鍵字的有序序列,一個無序序列可以透過建構一棵二元搜尋樹變成一個有序序列,建構樹的過程即為對無序序列進行尋找的過程。每次插入的新的結點都是二元搜尋樹上新的葉子結點,在進行插入操作時,不必移動其它結點,只需改動某個結點的指標,由空變為非空即可。搜尋、插入、刪除的複雜度等於樹高,期望O(㏒ n),最壞退化為偏斜二元樹O(n)。對於可能形成偏斜二元樹的問題可以經由樹高改良後的平衡樹將搜尋、插入、刪除的時間複雜度都維持在O(㏒ n),如AVL樹、紅黑樹等。
二元樹的典型圖形表示本質上是一棵倒置的樹。它以根節點開始,其中包含原始鍵值,根節點有兩個子節點;每個子節點可能有自己的子節點,理想情況下,樹的結構應使其成為完美平衡的樹,每個節點的左側和右側都有相同數量的子節點,完美平衡的樹可以實現最快的平均資料插入或資料取回,最壞的情況是一棵樹,其中每個節點只有一個子節點,因此就速度而言,它就像一個鏈結串列,二元樹的典型表示如下:
10 / \ 6 14 / \ / \ 5 8 11 18
儲存10的節點,此處僅表示為10,為根節點,連結左右子節點,左側節點儲存的值小於父節點,右側節點儲存的值大於父節點的值,父節點,請注意,如果刪除根節點和右子節點,則儲存值 6 的節點將相當於一棵新的、較小的二元樹,
二元樹的結構使得插入和搜尋功能易於使用遞迴實作。
事實上,插入和搜尋這兩個功能也非常相似。要將資料插入二元樹,需要一個函數在樹中的適當位置搜尋未使用的節點以插入鍵值。插入函數通常是一個遞迴函數,它繼續向下移動二元樹的級別,直到在遵循放置節點規則的位置處出現未使用的葉子為止。規則是較小的值應位於節點的左側,而較大或等於的值應位於節點的右側。按照規則,插入函數應該檢查每個節點以查看它是否為空,如果是,它將插入要與鍵值一起儲存的資料(在大多數實作中,空節點只是來自父節點,因此函數也必須創建該節點)。如果節點已經被填充,則插入函數應檢查要插入的鍵值是否小於目前節點的鍵值,如果是,則應在左子節點上遞迴呼叫插入函數,或者如果要插入的鍵值大於或等於當前節點的鍵值,則應在右子節點上遞迴呼叫插入函數。搜尋功能的工作方式類似。它應該檢查當前節點的鍵值是否是要搜尋的值。如果不是,則應檢查要搜尋的值是否小於該節點的值,在這種情況下,應在左子節點上被遞迴呼叫,或者是否大於該節點的值,它應該在右子節點上被遞迴呼叫,當然,在呼叫節點上的函數之前,還需要檢查以確保左或右子節點確實存在。
由於二元樹有㏒ (base 2) n 層,因此二元樹的平均搜尋時間為 ㏒ (base 2) n,要填滿整個二元樹並排序,大約需要 ㏒ (base 2) n * n,讓我們來看看簡單實作二元樹所需的程式碼。首先,必須有一個結構或類別定義為節點。
struct node
{
int key_value;
struct node *left;
struct node *right;
};
結構node能夠儲存 key_value 並包含兩個子節點,這兩個子節點將節點定義為樹的一部分,事實上,節點本身與鏈結串列中的節點非常相似,鏈結串列程式碼的基本知識對於理解二元樹的技術非常有幫助,基本上,指標是允許在樹中任意建立新節點所必需的。
二元樹有幾個重要的操作,包括插入元素、搜尋元素、刪除元素和刪除樹,我們將在這次教學內容中介紹這四個操作中的三個,將刪除元素留到稍後進行。
我們還需要追蹤二元樹的根節點,這將使我們能夠存取其餘資料:
struct node *root = 0;
有必要將 root 初始化為 0,以便其他函數能夠辨識出樹尚不存在,下面顯示的 destroy_tree 實際上會釋放儲存在節點 leaf: 樹下的樹中的所有節點。
void destroy_tree(struct node *leaf)
{
if( leaf != 0 )
{
destroy_tree(leaf->left);
destroy_tree(leaf->right);
free( leaf );
}
}
函數 destroy_tree 會轉到樹的每個部分的底部,即在存在非空節點時進行搜尋,刪除該葉子,然後再返回,函數從最左邊節點的父節點中刪除最左邊的節點,然後刪除右邊的子節點,然後刪除父節點,然後返回刪除剛剛刪除的節點的父節點的另一個子節點,然後繼續此刪除會一直進行到最初呼叫delete_tree 的樹節點。在上面的範例樹中,刪除節點的順序為 5 8 6 11 18 14 10,注意,需要刪除所有子節點以避免浪費記憶體。
如果需要,以下插入函數將建立一棵新樹;它依靠指向指標的指標來處理不存在樹的情況(根指向 NULL)。特別是,透過使用指向指標的指標,如果根指標為 NULL,則可以分配記憶體。
insert(int key, struct node **leaf)
{
if( *leaf == 0 )
{
*leaf = (struct node*) malloc( sizeof( struct node ) );
(*leaf)->key_value = key;
/* initialize the children to null */
(*leaf)->left = 0;
(*leaf)->right = 0;
}
else if(key < (*leaf)->key_value)
{
insert( key, &(*leaf)->left );
}
else if(key > (*leaf)->key_value)
{
insert( key, &(*leaf)->right );
}
}
插入函數按照規定的規則,沿著子節點樹向下移動進行搜尋,向左插入較小的值,向右插入較大的值,直到到達NULL 節點(一個空節點),並為該節點分配記憶體,並使用鍵值進行初始化,同時將新節點的子節點指標設為 NULL,建立新節點後,插入函數將不再呼叫自身,另請注意,如果該元素已在樹中,則不會將其添加兩次。
struct node *search(int key, struct node *leaf)
{
if( leaf != 0 )
{
if(key==leaf->key_value)
{
return leaf;
}
else if(key<leaf->key_value)
{
return search(key, leaf->left);
}
else
{
return search(key, leaf->right);
}
}
else return 0;
}
上面顯示的搜尋函數遞迴地沿著樹向下移動,直到它到達一個鍵值等於函數正在搜尋的值的節點,或者直到函數到達一個未初始化的節點,這意味著正在搜尋的值不會儲存在二元樹。它傳回一個指向呼叫它的函數的前一個實例的節點的指標。
平衡樹
平衡樹是電腦科學中的一類資料結構,為改進的二元搜尋樹。一般的二元搜尋樹的查詢複雜度取決於目標結點到樹根的距離(即深度),因此當結點的深度普遍較大時,查詢的均攤複雜度會上升。為了實現更高效的查詢,產生了平衡樹。在這裡,平衡指所有葉子的深度趨於平衡,更廣義的是指在樹上所有可能尋找的均攤複雜度偏低。
高度平衡樹
AVL樹(Adelson-Velsky and Landis Tree)是電腦科學中最早被發明的自平衡二元搜尋樹。在AVL樹中,任一節點對應的兩棵子樹的最大高度差為1,因此它也被稱為高度平衡樹。尋找、插入和刪除在平均和最壞情況下的時間複雜度都是O(㏒ n)。增加和刪除元素的操作則可能需要藉由一次或多次樹旋轉,以實現樹的重新平衡。AVL樹得名於它的發明者G. M. Adelson-Velsky和Evgenii Landis,他們在1962年的論文《An algorithm for the organization of information》中公開了這一資料結構。
節點的平衡因子是它的左子樹的高度減去它的右子樹的高度(有時相反)。帶有平衡因子1、0或 -1的節點被認為是平衡的。帶有平衡因子 -2或2的節點被認為是不平衡的,並需要重新平衡這個樹。平衡因子可以直接儲存在每個節點中,或從可能儲存在節點中的子樹高度計算出來。
要操作AVL Tree需要透過幾項資訊來做到,分別是計算節點高度(height)、計算Balance factor與理解什麼是高度平衡樹
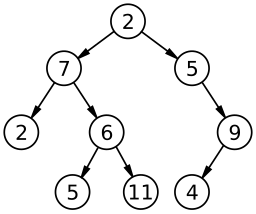
1. 節點(Node)的高度(height)
Height of node: Length of the longest path from it to the leaf
height = max( leftChildHeight, rightChildHeight) + 1
子節點為 null 時,高度視為 -1,其餘就是左右子節點中,最大的高度 + 1即為當前節點高度。
如下圖,標註了各個節點的高度
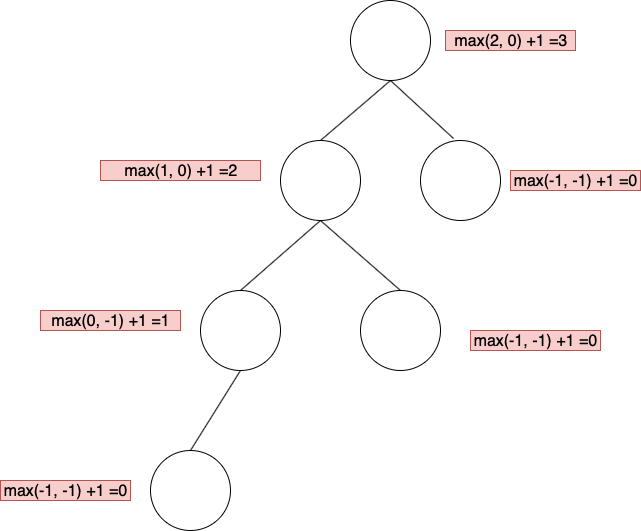
2. Balance Factor of T, BF(T)
For node T in a binary search tree is defined to be HL-HR, where HL and HR respectively, are the heights of the left and right subtree of T.
簡單來說就是計算出節點 T的左右子節點高度後相減,即為balance factor
balance factor有以下特性:
BF(T) < -1:右邊subtree比較重,需要將一些右邊節點往左邊調整
-1 <= BF(T) <= 1:表示平衡,暫時不用調整
BF(T) > 1:左邊subtree比較重,需要將一些左邊節點往右邊調整
如下圖,可以計算各個節點上的BF
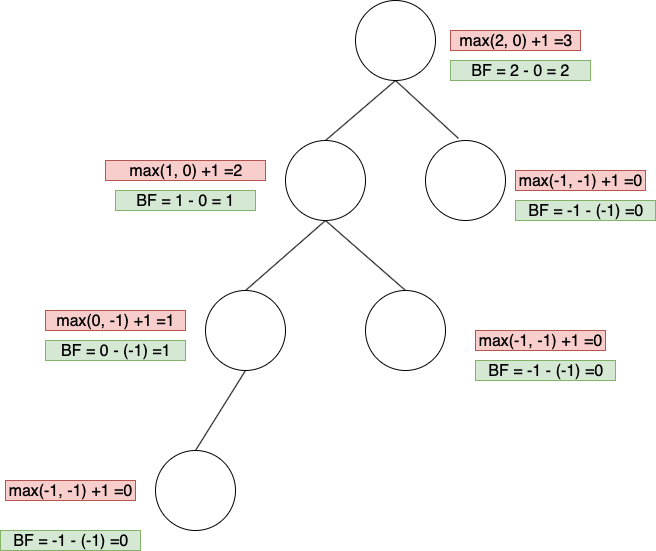
3. 高度平衡:
hight-balanced:
- Empty tree is height-balance
- If T is a nonempty binary tree with TL and TR as left and right subtrees respectively, T is hight-balanced iff
- TL and TR are height-balanced
- Math.abs( HL – HR) <= 1 where HL and HR are the height of TL and TR respectively.
這是AVL tree最主要的目的,簡單來說,要判斷一個二元樹是否平衡的方式,就是計算 root 左右節點的高度,得到高度後相減,如果得到的結果 < -1或 > 1,則表示這棵樹有某一側比較重,處於不平衡的狀態,需要調整來讓樹繼續維持平衡。
下面這張圖標為綠色的節點,或是 subtree,表示為balance,標為紅色的部分表示不平衡,需要做調整。
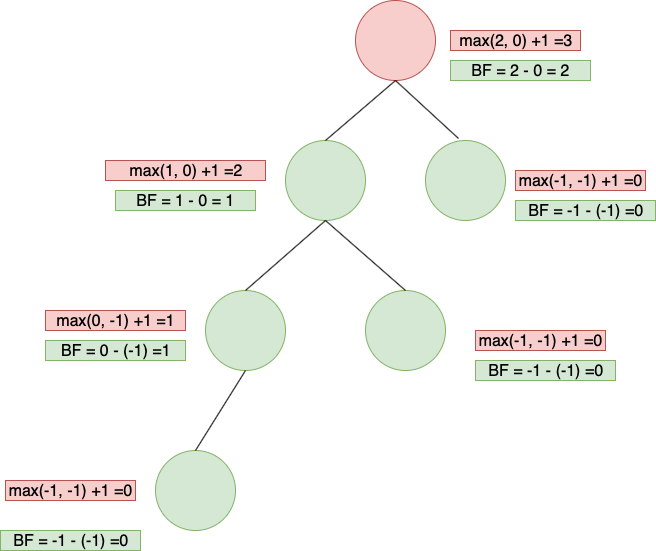
今天教學分享到這,你可以學到用C語言寫二元樹,你也可以判斷二元搜尋樹是不是高度平衡樹,就可以處理112 年公務人員初等考考試試題統計類科的資料處理大意我說的那個問題,下面還有一些相關文件可以索引閱讀,如果覺得有幫助就按讚一下,如果沒有看到你要的,也可以留言發問,感謝你的閱讀。
★編譯器資源
- 編譯器
- 設定C和C++ Code::Blocks編譯器的初學者教學指南:如果你苦惱的是編譯器的使用,可以看看設定C和C++ Code::Blocks編譯器的初學者教學指南。
- Code::Blocks 13.12 繁體中文化:如果想要使用code block 中文的朋友可以繼續閱讀Code::Blocks 13.12 繁體中文化,這裡不會有code block中文亂碼的問題。
- 設定Dev-C++ 5.11和MinGW-w64, Windows上免費的C跟C++編譯器
- C跟C++的Apple XCode
- g++簡介
- 使用Microsoft Visual C++ 2010 Express編譯GTK+
- Eclipse+CDT+MinGW 安裝測試
- 編譯器gcc
- Code::Blocks 20.03的安裝設定及繁體中文化




1 則留言